Dot Product Formula
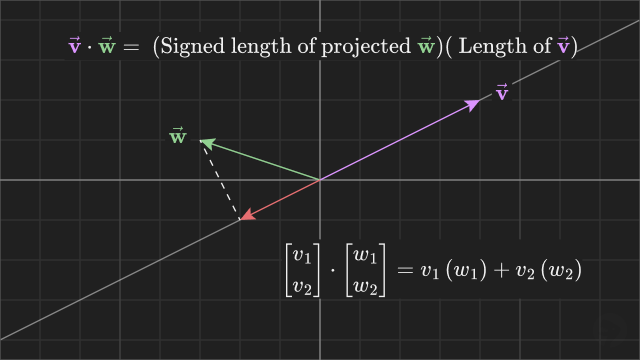
This formula calculates the dot product of two vectors. Geometrically, the result can be interpretted as the product of the signed length of the projected vector with the length of the first vector.
Formula Terms
| Expression | Description |
|---|---|
| The first vector. | |
| The second vector. | |
| The summation operator. | |
| The number of elements in the vectors. | |
| The -th element of the first vector. | |
| The -th element of the second vector. |
To calculate the dot product of two vectors, multiply the corresponding elements and then sum together the products. For example, to calculate the dot product of the vectors and , multiply the corresponding elements and then sum together the products like this:
Geometrically, the dot product can be interpretted as projecting the second vector onto the line of the first vector and then multiplying the positive or negative magnitude of the projected vector with the magnitude of the first vector to get the resulting number.
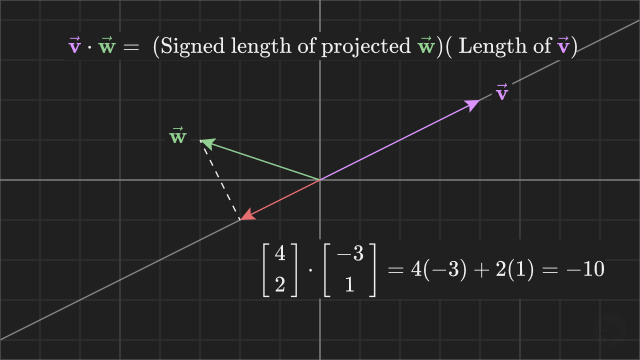
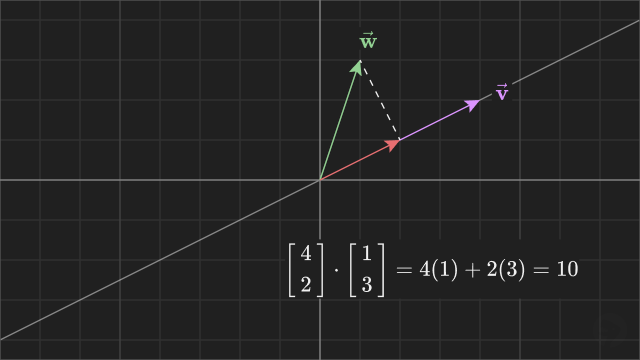
When the projected vector points in the opposite direction, like in the example above, the sign is negative. When the vectors point in the same direction, like in the example below, the dot product is positive.
And, when the vectors are perpendicular, the dot product is zero.
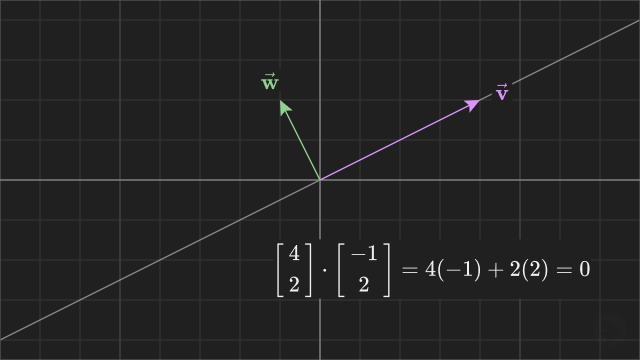
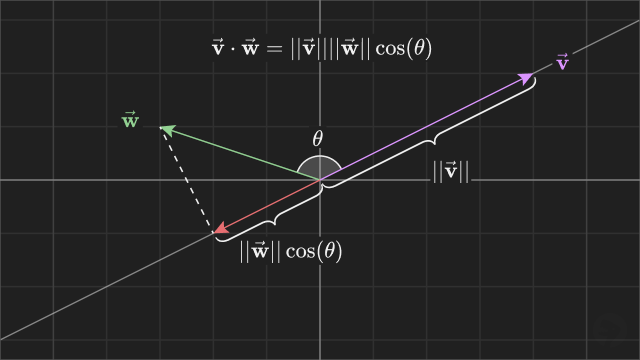
There is another formula for the dot product that gives us intuition for the result of the dot product. While the algebraic formula is usually how the dot product is computed, this formula explicitly defines the signed magnitude of the projected vector in terms of the angle between the two vectors.
The length of the projected vector is equal to , where is the angle between the two vectors. This is shown in the diagram below.
The magnitude of a vector is given by the square root of the sum of its components squared.
To calculate the unsigned angle between two vectors you can use the arc cosine function. This formula calculates angles between 0 and π (pi).
The cross product of two vectors in three dimensions produces a vector perpendicular to the two vectors and whose length is eual to the area betwee the two vectors.