Area Between Two Vectors 2D Formula
This formula calculates the area of the parallelogram between two vectors in two dimensions.
Formula Terms
| Expression | Description |
|---|---|
| The area of the parallelogram between the vectors. | |
| The first vector. | |
| The second vector. |
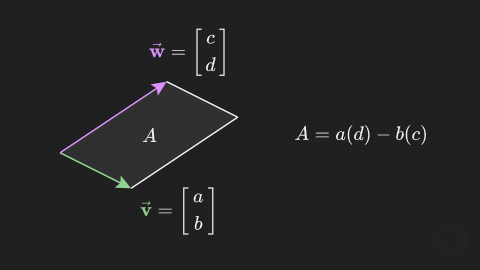
To calculate the area of the parallelogram between two vectors in two dimensions, take the cross product of the two vectors. For example, the area of the parallelogram between and is given by the formula below.
This expression calculates the signed area between the two vectors. If the second vector is a counterclockwise rotation from the first vector, as shown in the diagram below,the area is positive.

If the second vector is a clockwise rotation from the first vector, as shown in the diagram below, the area is negative.

There are a couple ways to arrive at this formula. You can think about the two vectors as living in three dimensions, in which case their cross product returns another vector that is parallel to the plane and whose length is equal to the area between the two vectors.
Alternatively, you can derive the formula by taking the determinant of the matrix whose columns are the same as the vectors. Since the determinant measures the change in area between the basis vectors and the column vectors, this gives us the same formula for the area.
In either case, this version of the formula calculates the signed area between the two vectors. The area is positive if the second vector is a counterclockwise rotation from the first and negative if its a clockwise rotation from the first.
The area between two vectors in three dimensions is given by the magnitude of their cross product.
The 3D formula returns the unsigned area, because the magnitude always returns a positive number.
The cross product of two vectors in 2D is calculated by the determinant of the corresponding 2x2 matrix. Geometrically the cross product corresponds to the signed area of the parallelogram formed between the two vectors.
The cross product of two vectors in three dimensions produces a vector perpendicular to the two vectors and whose length is eual to the area betwee the two vectors.